BP神经网络

人工神经网络(Artificial Neural Network,简称 ANN)是利用仿生原理对人脑神经网络的结构和功能的简化抽象。人工神经网络是一种可以并行分散处理数据，具有非线性映射、容错能力强、自适应学习进化的特点。BP人工神经网络是在此基础上，基于误差反向传播算法而设计的多层前向神经网络。因其能够实现输入与输出间任意的非线性映射，因此在模式识别、自适应控制、风险评估等领域有着广泛的应用。

BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络。

BP神经网络的基本原理

BP算法在神经网络训练中是一个十分典型的学习算法。其构成如下：一个输入层，一个或者多个隐含层和一个输出层构成，各层又由若干个神经元节点构成，每个神经元的输出值由其输入值、传递函数、阈值所决定。神经网络的学习过程包括了正向传播和反向传播两个过程。正向传播的过程中，在输入层输出数据，经过隐含层一系列运算后，将输出层得到的结果与期望值比较，得到误差取值。若误差大于某个范围则进行反向传播，根据上一层的误差，对该层神经元的权值和阈值进行相应的修改，从而减小误差。如此循环，直到误差在精度范围内或者达到训练终止条件为止。

BP神经网络的训练方法

BP神经网络的基本训练步骤如下：

  1. BP神经网络的构建和初始化，确定隐含层层数，确定各层的节点数，随机生成各个节点的权值和阈值；
  2. 输入训练数据集，训练输入数据以及其对应的输出数据；
  3. 根据输入样本计算输出数据；
  4. 根据输出数据和期望数据计算误差，并判定是否达到精度，若达到精度就停止运行并取得各节点权值和阈值，否则继续执行（5）；
  5. 根据误差反向传播，修正各层各节点的权值和阈值；
  6. 继续执行（3）。

基本BP神经网络的构建与训练（Python）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import numpy as np

#sigmoid 激活函数
def sigmoid1(x):
	a=1/(1+np.exp(-x))
	return a

#训练集
training_set=np.array([[1,1,0],[1,0,1],[0,1,1],[0,0,0]])
yy=np.zeros((4,1))
eta=0.1

#定义连接权、阈值
vih=np.random.rand(2,2)	#输入层与隐层连接权
delt_vih=np.zeros((2,2))
r=np.random.rand(1,2)	#隐层阈值
delt_r=np.zeros((1,2))
whj=np.random.rand(2,1)	#隐层与输出层连接权
delt_whj=np.zeros((2,1))
o=np.random.rand(1,1)	#输出层阈值
delt_o=np.zeros((1,1))
#创建隐层

alph=np.zeros((1,2))
b=np.zeros((1,2))
e=np.zeros((1,2))	#隐层梯度项
#创建输出层
beita=np.zeros((1,1))
y=np.zeros((1,1))
g=np.zeros((1,1))	#输出层梯度项
#开始训练
times=input(How many times do you want to train:\n)
times=int(times)
for daishu in range(0,times):
	for train in range(0,4):
	#计算隐层的输入
	alph[0,0]=vih[0,0]*training_set[train,0]+vih[1,0]*training_set[train,1]
	alph[0,1]=vih[0,1]*training_set[train,0]+vih[1,1]*training_set[train,1]
	#计算隐层输出
	b[0,0]=sigmoid1(alph[0,0]-r[0,0])
	b[0,1]=sigmoid1(alph[0,1]-r[0,1])
	#计算输出层的输入
	beita[0,0]=whj[0,0]*b[0,0]+whj[1,0]*b[0,1]
	#输出层输出
	y[0,0]=sigmoid1(beita[0,0]-o[0,0])
	yy[train,0]=y[0,0]
	#输出层梯度项
	g[0,0]=y[0,0]*(1-y[0,0])*(training_set[train,2]-y[0,0])
	#隐层梯度项
	e[0,0]=b[0,0]*(1-b[0,0])*(whj[0,0]*g[0,0])
	e[0,1]=b[0,1]*(1-b[0,1])*(whj[1,0]*g[0,0])
	#更新连接权和阈值
	delt_whj[0,0]=eta*g[0,0]*b[0,0]
	delt_whj[1,0]=eta*g[0,0]*b[0,1]
	whj[0,0]=delt_whj[0,0]+whj[0,0]
	whj[1,0]=delt_whj[1,0]+whj[1,0]
	delt_o[0,0]=-(eta*g[0,0])
	o[0,0]=delt_o[0,0]+o[0,0]
	delt_vih[0,0]=eta*e[0,0]*training_set[train,0]
	delt_vih[1,0]=eta*e[0,0]*training_set[train,1]
	delt_vih[0,1]=eta*e[0,1]*training_set[train,0]
	delt_vih[1,1]=eta*e[0,1]*training_set[train,1]
	vih[0,0]=vih[0,0]+delt_vih[0,0]
	vih[1,0]=vih[1,0]+delt_vih[1,0]
	vih[0,1]=vih[0,1]+delt_vih[0,1]
	vih[1,1]=vih[1,1]+delt_vih[1,1]
	delt_r[0,0]=-(eta*e[0,0])
	delt_r[0,1]=-(eta*e[0,1])
	r[0,0]=delt_r[0,0]+r[0,0]
	r[0,1]=delt_r[0,1]+r[0,1]

training_set=training_set.astype(np.float64)
training_set[:,2]=yy[:,0]
print(Output:)
print(training_set)

测试结果如下：

/

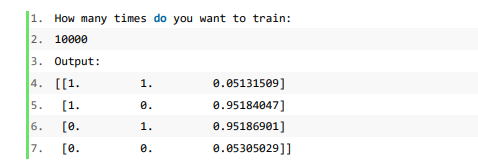
BP神经网络函数逼近实验

网络构建模型：

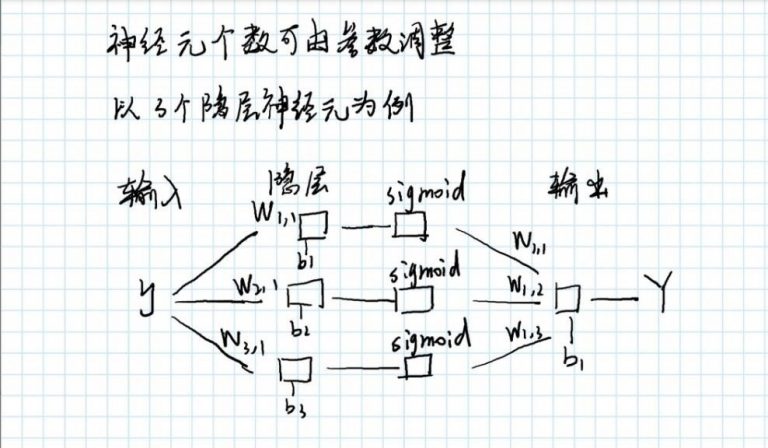神经网络模型

对函数 f(x)=x2/3 +0.9√(3.3-x2 )×sin(31.41593x)的拟合（Python ）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
import numpy as np
import math
import matplotlib.pyplot as plt
import time
#计时
start=time.time()
# 取得样本
x = np.linspace(-1.81659,1.81659,100)#获取-10 到 10 之间距离相等的 10000 个点，作为 x 取值。
x_size = x.size
y = np.zeros((x_size,1))#生成 y 数组
for i in range(x_size):
	y[i]= math.pow(math.pow(x[i],2),1/3)+0.9*math.pow((3.3-
math.pow(x[i],2)),0.5)*math.sin(10*math.pi*x[i])#得到样本集

#网络参数
hidesize = 5 #隐层神经元个数
W1 = np.random.random((hidesize,1)) #输入层与隐层之间的权重
B1 = np.random.random((hidesize,1)) #隐含层神经元的阈值
W2 = np.random.random((1,hidesize)) #隐含层与输出层之间的权重
B2 = np.random.random((1,1)) #输出层神经元的阈值
threshold = 0.05#速率
max_steps = 1001#训练次数
def sigmoid(x_):#激活函数
	y_ = 1/(1+math.exp(-x_))
	return y_

#开始训练
E = np.zeros((max_steps,1))#误差随迭代次数的变化
Y = np.zeros((x_size,1)) # 模型的输出结果
for k in range(max_steps):
	temp = 0
	for i in range(x_size):

	#正向传播
	hide_in = np.dot(x[i],W1)-B1 # 隐含层输入数据
	hide_out = np.zeros((hidesize,1)) #隐含层的输出数据
	for j in range(hidesize):
	hide_out[j] = sigmoid(hide_in[j])
	y_out = np.dot(W2,hide_out) - B2 #模型输出
	Y[i] = y_out
	e = y_out - y[i] #模型输出减去实际结果。得出误差

	#反向传播
	dB2 = -1*threshold*e#输出层阈值误差
	dW2 = e*threshold*np.transpose(hide_out)#输出层权值误差
	dB1 = np.zeros((hidesize,1))#输入层阈值误差
	for j in range(hidesize):
	dB1[j] = np.dot(np.dot(W2[0][j],sigmoid(hide_in[j])),(1-sigmoid(hide_in[j]))*(-
*e*threshold)
	dW1 = np.zeros((hidesize,1))#输出层权值误差
	for j in range(hidesize):
	dW1[j] = np.dot(np.dot(W2[0][j],sigmoid(hide_in[j])),(1-
sigmoid(hide_in[j]))*x[i]*e*threshold)
#参数修正
W1 = W1 - dW1
B1 = B1 - dB1
W2 = W2 - dW2
B2 = B2 - dB2
temp = temp + abs(e)

E[k] = temp
#训练进度
if k%100==0:
print('已训练%d 次'%k)
stop=time.time()
print('训练用时%ds'%(stop-start))

#训练结果
print('输入层权值 w1：')
print(W1)
print('输入层阈值 b1：')
print(B1)
print('输出层权值 w2：')
print(W2)
print('输出层阈值 b2：')
print(B2)
#拟合曲线
plt.figure()
plt.plot(x,y)
plt.plot(x,Y,color='red',linestyle='--')

plt.show()
#误差变化
steps = np.linspace(0,max_steps,max_steps)
plt.figure()
plt.plot(steps,E)
plt.show()

第一组测试结果：

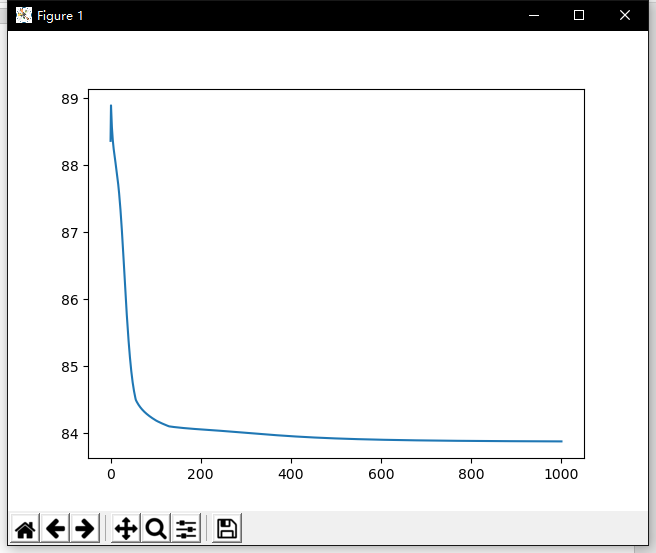
样本数量 100，训练次数 1000，训练速率 0.05

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
已训练 0 次
训练用时 0s
已训练 100 次
训练用时 1s
已训练 200 次
训练用时 2s
已训练 300 次
训练用时 3s
已训练 400 次
训练用时 4s
已训练 500 次
训练用时 5s
已训练 600 次
训练用时 6s
已训练 700 次
训练用时 8s
已训练 800 次
训练用时 9s
已训练 900 次
训练用时 10s
已训练 1000 次
训练用时 11s
输入层权值 w1：
[[ 3.12169479]
[-0.12887541]
[-3.3705294 ]
[ 0.68280681]
[-0.15176392]]
输入层阈值 b1：
[[2.41933289]
[2.5423254 ]
[2.67626102]
[2.92251419]
[2.58144723]]			
输出层权值 w2：
[[1.25280733]
[0.07273052]
[1.29053161]
[0.28913382]
[0.09012128]]
输出层阈值 b2：
[[-0.13334891]]

拟合曲线：

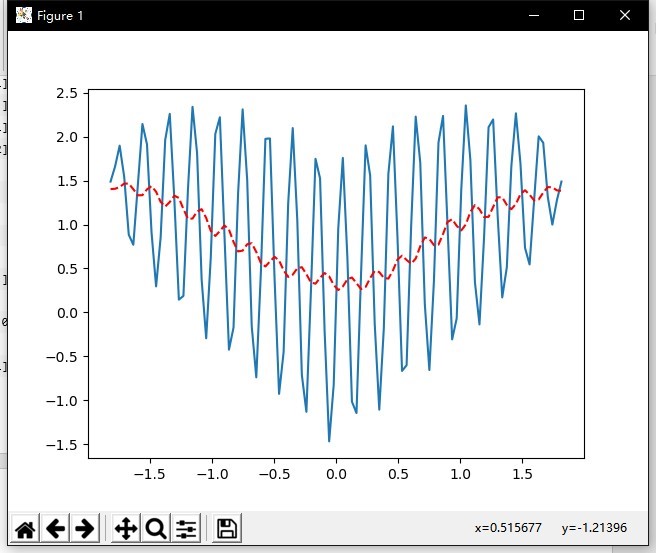
拟合曲线-1

误差曲线：

误差曲线-1

第二组测试结果：

样本数量 10000，训练次数 1000，训练速率 0.05

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
已训练 0 次
训练用时 1s
已训练 100 次
训练用时 114s
已训练 200 次
训练用时 227s

已训练 300 次
训练用时 341s
已训练 400 次
训练用时 454s
已训练 500 次
训练用时 567s
已训练 600 次
训练用时 680s
已训练 700 次
训练用时 793s
已训练 800 次
训练用时 907s
已训练 900 次
训练用时 1020s
已训练 1000 次
训练用时 1134s
输入层权值 w1：
[[-9.34109363]
[-6.26655843]
[ 0.38915887]
[-2.666515 ]
[-2.69118967]]
输入层阈值 b1：
[[ 1.47712007]
[ 4.86462404]
[-2.89037925]
[ 1.12851018]
[ 1.31828715]]
输出层权值 w2：
[[3.28226408]
[4.90921857]
[4.96920982]
[-4.36115203]
[-4.59367305]]
输出层阈值 b2：
[[3.29980763]]

拟合曲线：

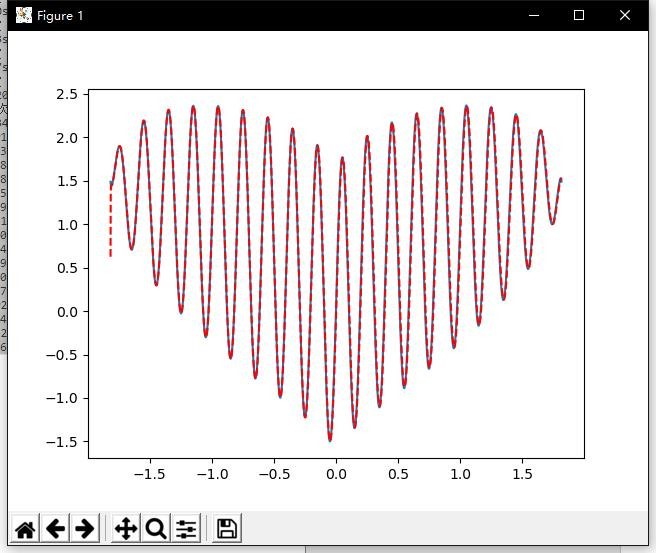
拟合曲线-2

误差曲线：

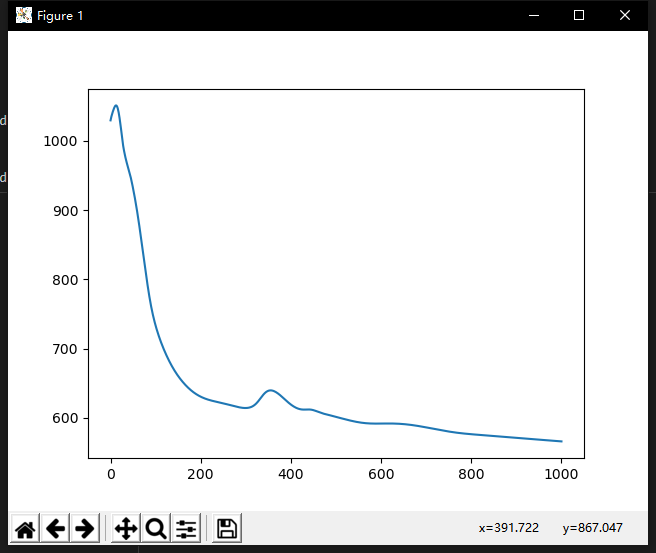
误差曲线-2

技术 > Algorithm > AI
#ai #nn #pnn #algorithm
BP神经网络
https://jason-xy.github.io/2020/06/bpnn/
作者
Jason Hsu
发布于
2020年6月19日
许可协议