「Icoding题解」平衡二叉树(AVL)的插入算法

AVL添加

题目链接

平衡二叉树，是一种二叉排序树，其中每个结点的左子树和右子树的高度差至多等于1。它是一种高度平衡的二叉排序树。现二叉平衡树结点定义如下：

typedef struct node
{
    int val;
    struct node *left;
    struct node *right;
    struct node *parent;
    int height;
} node_t;

请实现平衡二叉树的插入算法：

//向根为 root 的平衡二叉树插入新元素 val，成功后返回新平衡二叉树根结点
node_t *avl_insert(node_t *root, int val);

前置知识

AVL定义

平衡二叉搜索树:简称平衡二叉树。由前苏联的数学家Adelse-Velskil和Landis在1962年提出的高度平衡的二叉树，根据科学家的英文名也称为AVL树。它具有如下几个性质：

1. 可以是空树。
2. 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过1。

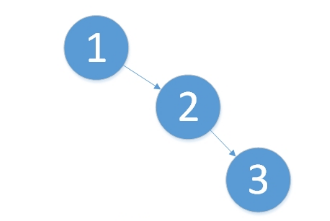
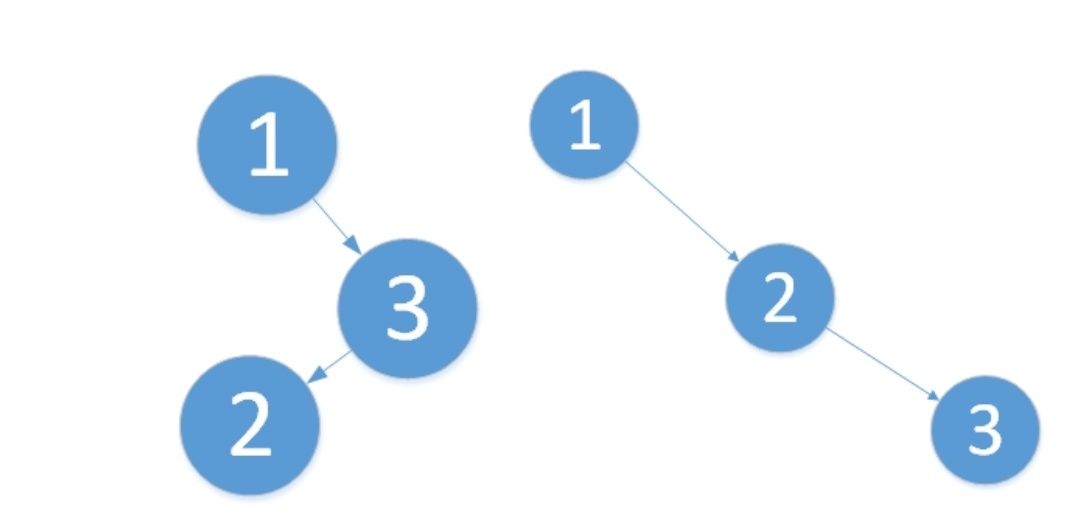
平衡之意，如天平，即两边的分量大约相同。如定义，假如一棵树的左右子树的高度之差超过1，如左子树的树高为2，右子树的树高为0，子树树高差的绝对值为2就打破了这个平衡。如依次插入1，2，3三个结点（如下图）后，根结点的右子树树高减去左子树树高为2，树就失去了平衡。

那么在建立树的过程中，我们如何知道左右子树的高度差呢？在这里我们采用了平衡因子进行记录。

平衡因子：左子树的高度减去右子树的高度。由平衡二叉树的定义可知，平衡因子的取值只可能为0,1,-1.分别对应着左右子树等高，左子树比较高，右子树比较高。

AVL树的插入时的失衡与调整

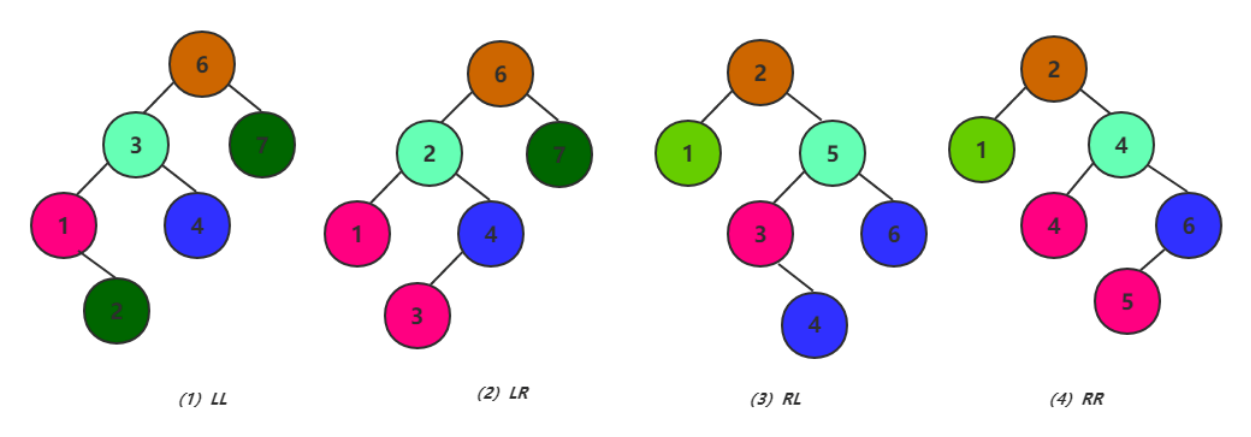
不平衡的4种情况

1. 6节点的左子树3节点高度比右子树7节点大2，左子树3节点的左子树1节点高度大于右子树4节点，这种情况成为左左。
2. 6节点的左子树2节点高度比右子树7节点大2，左子树2节点的左子树1节点高度小于右子树4节点，这种情况成为左右。
3. 2节点的左子树1节点高度比右子树5节点小2，右子树5节点的左子树3节点高度大于右子树6节点，这种情况成为右左。
4. 2节点的左子树1节点高度比右子树4节点小2，右子树4节点的左子树3节点高度小于右子树6节点，这种情况成为右右。

LL型

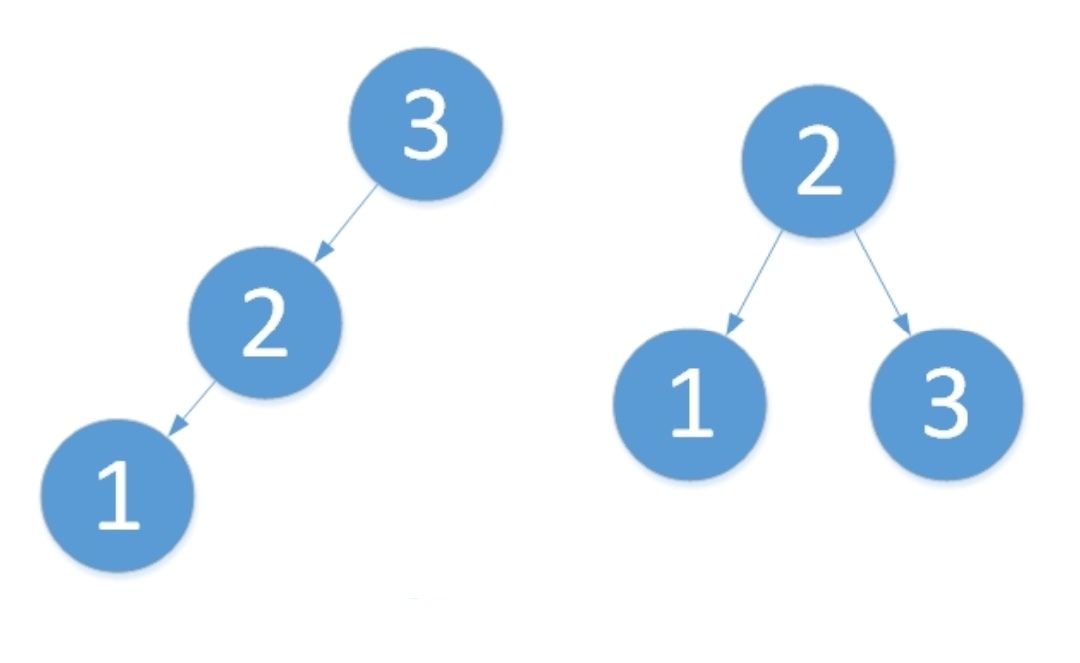
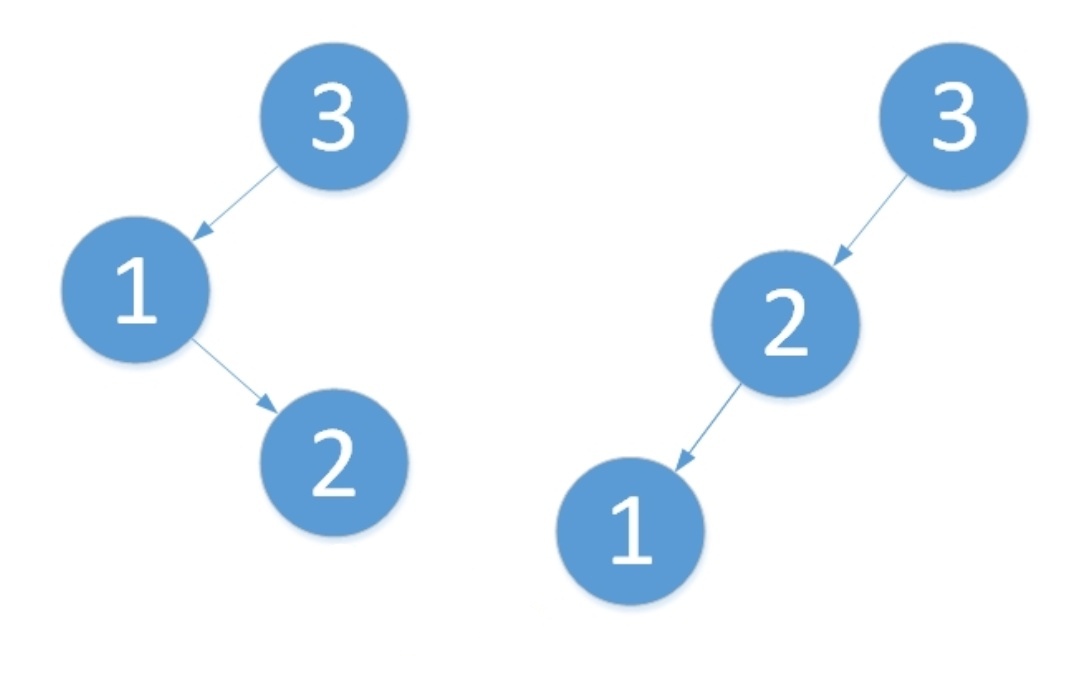
在LL型的不平衡树中，我们首先找到最小不平衡子树，再以其根结点向右旋转。为何是向右旋转呢？应该不难理解，向右旋转后，相当于右边的子树树高增加了1，而左边的子树树高降低了1，而原本的树高之差为2,那么就能够将根的平衡因子就化为0.引用一下之前的图如下。旋转之后为“原来根结点的左孩子作为新的根结点”。

我们对树以根结点为中心，向右旋转。旋转步骤如下:

1. 将2作为根结点。
2. 将3作为2的右孩子。
3. 将2的右孩子作为3的左孩子（维护树的有序性，只是此处为NULL而已）。

旋转后，3与2的平衡因子为0，1的平衡因子保持不变。

RR型

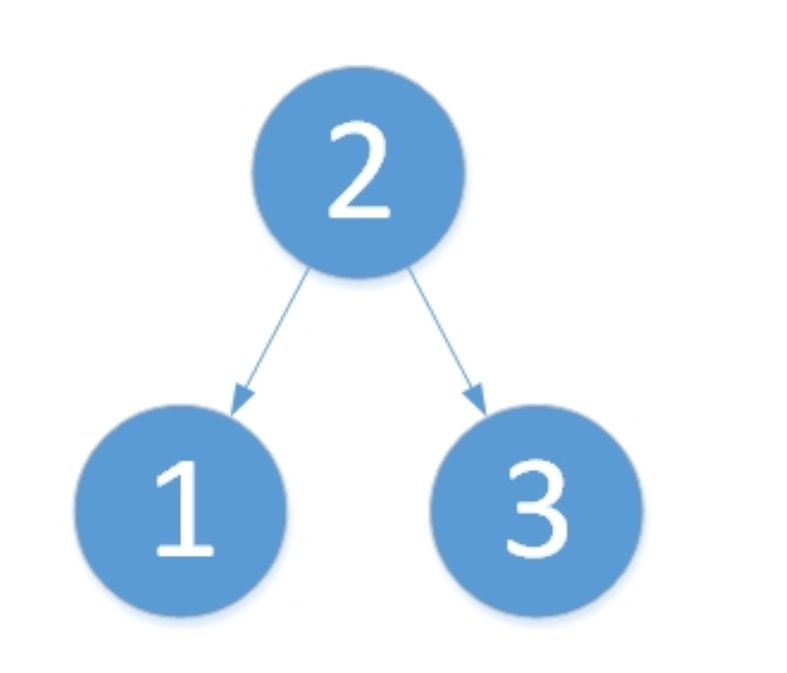
还是引用一下之前的例子。旋转之后为“原来根结点的右孩子作为新的根结点”。旋转的步骤如下：

1. 将2作为根结点。
2. 将1作为2的左孩子。
3. 将2的左孩子作为1的右孩子（维护树的有序性，只是此处为NULL而已）。

最后1,2,3的平衡因子都为0。

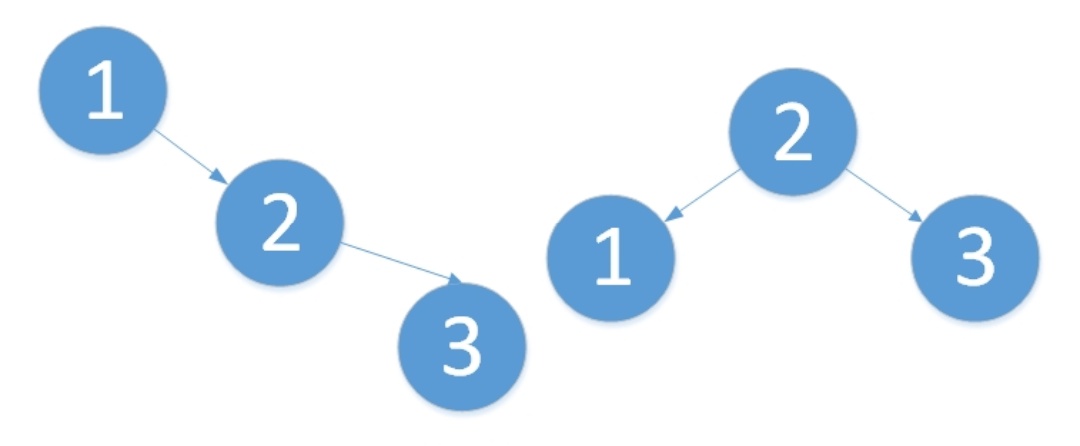
LR型

对于LR，要分为两步进行旋。旋转之后为“原来根结点的左孩子的右孩子作为新的根结点”。

第一以较高子树的根，即1，为中心向左旋转。具体步骤如下：

1. 将2的左子树作为1的右子树（维护树的有序性，只是此处为NULL而已）。
2. 将1作为2的左子树。
3. 将2作为3的左子树。

第二以原树的根，即3为中心，向右旋转。最后结果如下：

旋转后，1,2,3的平衡因子变为0。

RL型

还是引用一下之前的例子。与LR型类似，我们需要进行两次旋转。旋转之后为“原来根结点的右孩子的左孩子作为新的根结点”。

第一，以根结点的右孩子即3为中心向右旋转，结果如下。具体步骤如下：

1. 将2作为1的右孩子。
2. 将3作为2的右孩子。
3. 将2的右孩子作为3的左孩子（维护树的有序性，只是此处为NULL而已）。

第二，以原根结点即1，作为中心，向左旋转。结果如下。具体步骤如下：

1. 将2作为根结点。

2. 将1作为2的左孩子。

3. 将2的左孩子作为1的右孩子（维护树的有序性，只是此处为NULL而已）。

最后1,2,3的平衡因子都是0。

答案代码及注释

#include "avl.h"
#include <stdio.h>
#include <stdlib.h>

int getHeight(node_t* root)
{
    int height = 0;
    if (root)
        height = root->height;
    return height;
}
int getMax(int a, int b)
{
    return a > b ? a : b;
}
//LL型
node_t* LL(node_t* root)
{
    node_t* child = root->left;
    root->left = child->right;
    child->right = root;
    root->height = getMax(getHeight(root->left), getHeight(root->right)) + 1;
    child->height = getMax(getHeight(child->left), root->height) + 1;
    return child;
}
//RR型
node_t* RR(node_t* root)
{
    node_t* child = root->right;
    root->right = child->left;
    child->left = root;
    root->height = getMax(getHeight(root->left), getHeight(root->right)) + 1;
    child->height = getMax(root->height, getHeight(child->right)) + 1;
    return child;
}
//RL型
node_t* RL(node_t* root)
{
    //右左调整分两步,先LL再RR
    root->right = LL(root->right);
    return RR(root);
}
//LR型
node_t* LR(node_t* root)
{
    //左右调整分两步,先RR再LL
    root->left = RR(root->left);
    return LL(root);
}
node_t* NewNode(int val)
{
    node_t* newnode = (node_t*)malloc(sizeof(node_t));
    newnode->val = val;
    newnode->left = NULL;
    newnode->right = NULL;
    newnode->parent = NULL;
    newnode->height = 0;
    return newnode;
}
node_t* avl_insert(node_t* root, int val)
{
    if (!root)//如果avl不存在则先创建一个avl
        root = NewNode(val);
    else if (val < root->val) {
        //如果val小于根结点val,则插入左子树
        root->left = avl_insert(root->left, val);
        if (getHeight(root->left) - getHeight(root->right) == 2) {
            //插入后判断平衡因子,如果等于2则需要旋转
            if (val < root->left->val)//LL型
                root = LL(root);
            else//LR型
                root = LR(root);
        }
    } else if (val > root->val) {
        //如果val大于根结点val,则插入右子树
        root->right = avl_insert(root->right, val);
        if (getHeight(root->right) - getHeight(root->left) == 2) {
            //插入后判断平衡因子,如果等于2则需要旋转
            if (val > root->right->val)//RR型
                root = RR(root);
            else//RL型
                root = RL(root);
        }
    }
    root->height = getMax(getHeight(root->left), getHeight(root->right)) + 1;
    return root;
}