「LeetCode」—— 28.实现 strStr() —KMP算法

简介

KMP 算法是 D.E.Knuth、J,H,Morris 和 V.R.Pratt 三位神人共同提出的，称之为 Knuth-Morria-Pratt 算法，简称 KMP 算法。该算法相对于 Brute-Force（暴力）算法有比较大的改进，主要是消除了主串指针的回溯，从而使算法效率有了某种程度的提高。

提取加速匹配信息

基本思想

这一个视频讲解的比较简单易懂。

通过观看讲解，我们可以知道这里的重点就是生成next数组。

可以再参考一下《漫画算法》中小灰灰的讲解：

next 数组

next数组到底是个什么鬼呢？这是一个一维整型数组，数组的下标代表了“已匹配前缀的下一个位置”，元素的值则是“最长可匹配前缀子串的下一个位置”。

或许这样的描述有些晦涩，我们来看一下图：

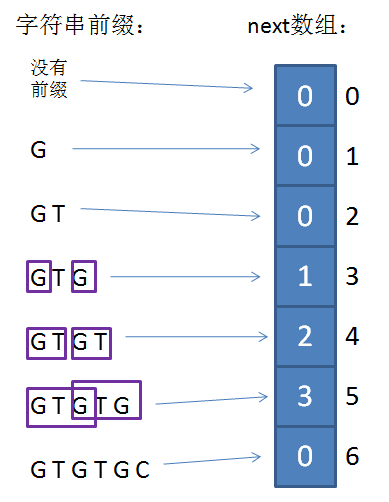
当模式串的第一个字符就和主串不匹配时，并不存在已匹配前缀子串，更不存在最长可匹配前缀子串。这种情况对应的next数组下标是0，next[0]的元素值也是0。

如果已匹配前缀是G、GT、GTGTGC，并不存在最长可匹配前缀子串，所以对应的next数组元素值（next[1]，next[2]，next[6]）同样是0。

GTG的最长可匹配前缀是G，对应数组中的next[3]，元素值是1。

以此类推，

GTGT 对应 next[4]，元素值是2。

GTGTG 对应 next[5]，元素值是3。

有了next数组，我们就可以通过已匹配前缀的下一个位置（坏字符位置），快速寻找到最长可匹配前缀的下一个位置，然后把这两个位置对齐。

比如下面的场景，我们通过坏字符下标5，可以找到next[5]=3，即最长可匹配前缀的下一个位置：

说完了next数组是什么，接下来我们再来思考一下，如何事先生成这个next数组呢？

由于已匹配前缀数组在主串和模式串当中是相同的，所以我们仅仅依据模式串，就足以生成next数组。

最简单的方法是从最长的前缀子串开始，把每一种可能情况都做一次比较。

假设模式串的长度是m，生成next数组所需的最大总比较次数是1+2+3+4+……+m-2 次。

显然，这种方法的效率非常低，如何进行优化呢？

我们可以采用类似“动态规划”的方法。首先next[0]和next[1]的值肯定是0，因为这时候不存在前缀子串；从next[2]开始，next数组的每一个元素都可以由上一个元素推导而来。

已知next[i]的值，如何推导出next[i+1]呢？让我们来演示一下上述next数组的填充过程：

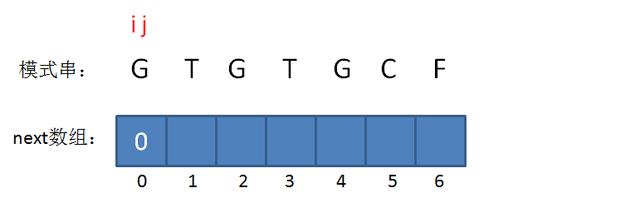
如图所示，我们设置两个变量i和j，其中i表示“已匹配前缀的下一个位置”，也就是待填充的数组下标，j表示“最长可匹配前缀子串的下一个位置”，也就是待填充的数组元素值。

当已匹配前缀不存在的时候，最长可匹配前缀子串当然也不存在，所以i=0，j=0，此时next[0] = 0。

接下来，我们让已匹配前缀子串的长度加1：

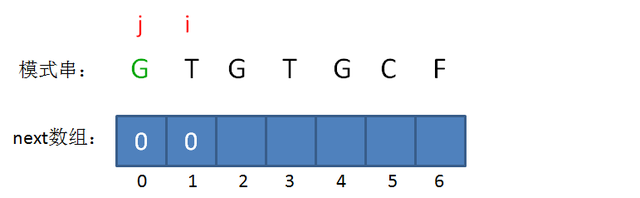
此时的已匹配前缀是G，由于只有一个字符，同样不存在最长可匹配前缀子串，所以i=1，j=0，next[1] = 0。

接下来，我们让已匹配前缀子串的长度继续加1：

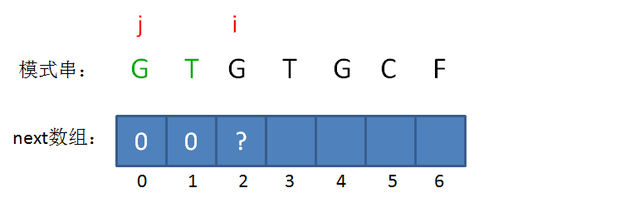
此时的已匹配前缀是GT，我们需要开始做判断了：由于模式串当中 pattern[j] != pattern[i-1]，即G！=T，最长可匹配前缀子串仍然不存在。

所以当i=2时，j仍然是0，next[2] = 0。

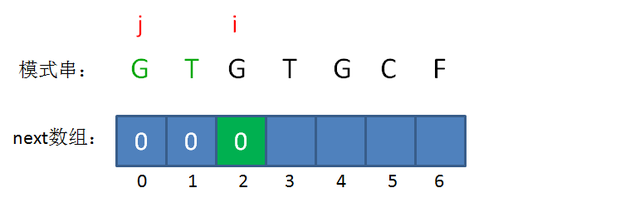
接下来，我们让已匹配前缀子串的长度继续加1：

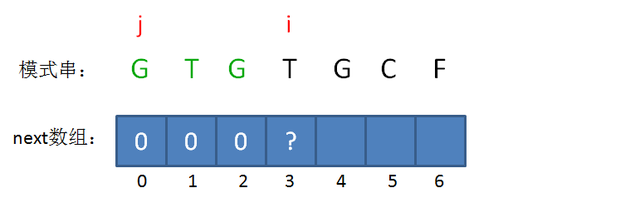
此时的已匹配前缀是GTG，由于模式串当中 pattern[j] = pattern[i-1]，即G=G，最长可匹配前缀子串出现了，是G。

所以当i=3时，j=1，next[3] = next[2]+1 = 1。

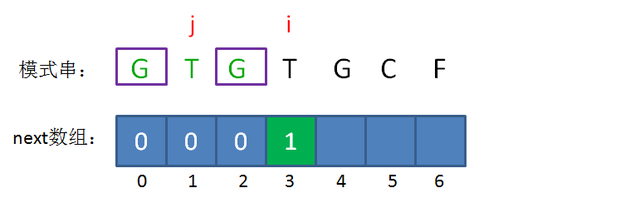
接下来，我们让已匹配前缀子串的长度继续加1：

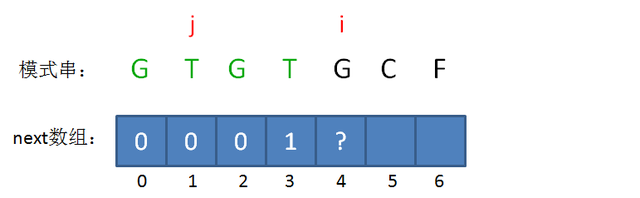
此时的已匹配前缀是GTGT，由于模式串当中 pattern[j] = pattern[i-1]，即T=T，最长可匹配前缀子串又增加了一位，是GT。

所以当i=4时，j=2，next[4] = next[3]+1 = 2。

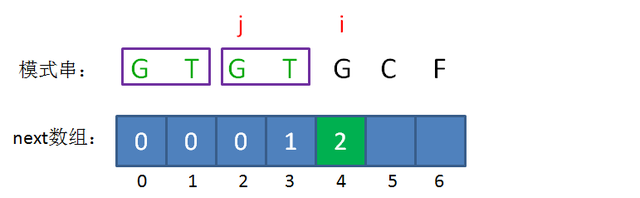
接下来，我们让已匹配前缀子串的长度继续加1：

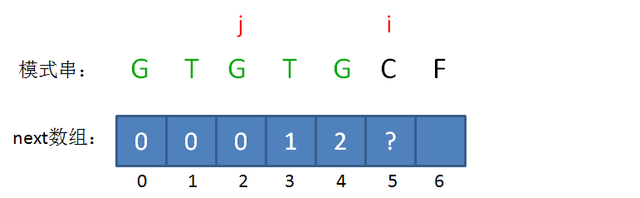
此时的已匹配前缀是GTGTG，由于模式串当中 pattern[j] = pattern[i-1]，即G=G，最长可匹配前缀子串又增加了一位，是GTG。

所以当i=5时，j=3，next[5] = next[4]+1 = 3。

接下来，我们让已匹配前缀子串的长度继续加1：

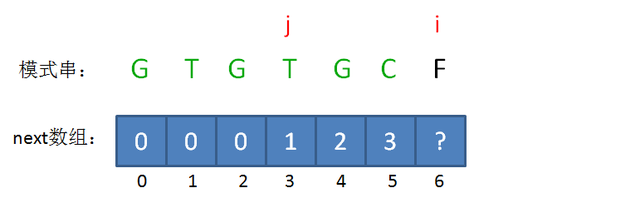
此时的已匹配前缀是GTGTGC，这时候需要注意了，模式串当中 pattern[j] ！= pattern[i-1]，即T != C，这时候该怎么办呢？

这时候，我们已经无法从next[5]的值来推导出next[6]，而字符C的前面又有两段重复的子串“GTG”。那么，我们能不能把问题转化一下？

或许听起来有些绕：我们可以把计算“GTGTGC”最长可匹配前缀子串的问题，转化成计算“GTGC”最长可匹配前缀子串的问题。

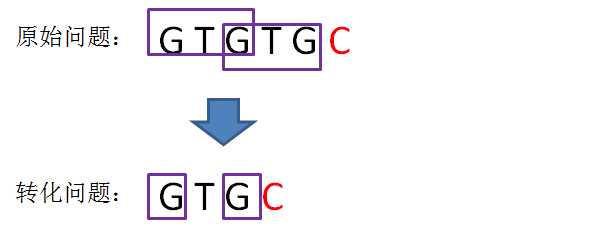
这样的问题转化，也就相当于把变量j回溯到了next[j]，也就是j=1的局面（i值不变）：

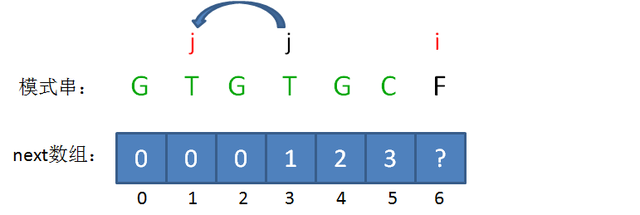
回溯后，情况仍然是 pattern[j] ！= pattern[i-1]，即T！=C。那么我们可以把问题继续进行转化：

问题再次的转化，相当于再一次把变量j回溯到了next[j]，也就是j=0的局面：

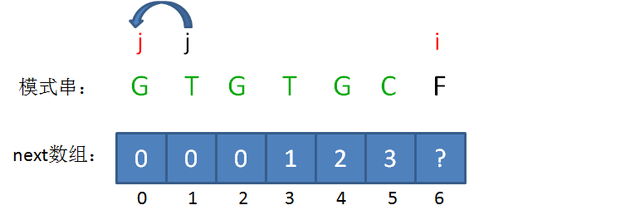
回溯后，情况仍然是 pattern[j] ！= pattern[i-1]，即G！=C。j已经不能再次回溯了，所以我们得出结论：i=6时，j=0，next[6] = 0。

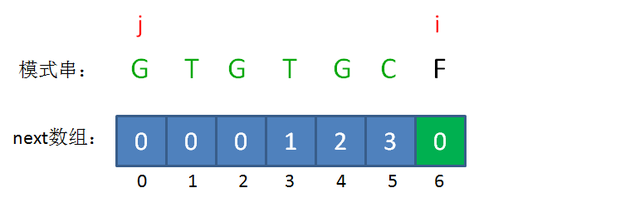
以上就是next数组元素的推导过程。

代码实现

get_next代码：

void get_next(char* string, int* next) {
    int i=0,j=-1;
    next[0]=-1;
    while (i<strlen(string)){
        if(j==-1||string[i]==string[j]){
            i++,j++;
            next[i]=j;
        }
        else
        j=next[j];
    }
}

这里字符数组的第0位是存放了字母的

这里重点解释一下当string[i]!=string[j]时的情况:

当匹配到第 i 和 j 失败时，next[j+1] < i，那么求 next[j+1] 就等同于求 string[j-i+1] ~ string[j] 与 string[0] ~ string[i-1] 的最长重合串，那么就相当于求 next[i]，即j=next[j]。

打印next数组代码

#include <stdio.h>
#include <string.h>

void get_next(char* string, int* next) {
    int i=0,j=-1;
    next[0]=-1;
    while (i<strlen(string)){
        if(j==-1||string[i]==string[j]){
            i++,j++;
            next[i]=j;
        }
        else
        j=next[j];
    }
}

int main(){
    char str[100]={"ababaaabbaba"};
    int next[100]={0};
    get_next(str, next);
    for(int i=0; i<strlen(str); i++){
        printf("%c\t",str[i]);
    }
    printf("\n");
    for(int i=0; i<strlen(str);i++){
        printf("%d\t",i);
    }
    printf("\n");
    for(int i=0; i<strlen(str);i++){
        printf("%d\t",next[i]);
    }
    return 0;
}

输出样例

a       b       a       b       a       a       a       b       b       a       b       a       ;
0       1       2       3       4       5       6       7       8       9       10      11		;
-1      0       0       1       2       3       1       1       2       0       1       2		;

题面

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

示例 1:

输入: haystack = "hello", needle = "ll"
输出: 2

示例 2:

输入: haystack = "aaaaa", needle = "bba"
输出: -1

说明:

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。

代码

void get_next(char* T, int *next)
{
	int j, k;
	j = 0;
	k = -1;
	next[0] = -1;
	while (j < strlen(T)){
		if (k == -1 || T[j] == T[k]){
			j++;
			k++;
			next[j] = k;
		}
		else{
			k = next[k];
		}
	}
}

//KMP算法
int KMP(char* S, char* T)
{
    if(T=="")return 0;
	int i = 0, j = 0,next[255]={0};
	get_next(T, next);
	int slen = strlen(S);
	int tlen = strlen(T);

	while (i < slen && j < tlen){
		if (j == -1 || S[i] == T[j]){
			i++;
			j++;
		}
		else{
			j = next[j];
		}
	}
	if (j == tlen){
		return i - tlen;
	}
	else{
		return -1;
	}
}